LeetCode 刷题

Last updated on 8 months ago

LeetCode 刷题

（以前刷的）

1.链表反转

  • 定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

​ 示例: 

1
2
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

限制： 

1
0 <= 节点个数 <= 5000

解法一 暴力：

​ 遍历链表的每个节点，每遍历个节点就用头插法插入一个新的链表里

​ 时间复杂度为 T(n^2) 空间复杂度为O(n)

解法二： 迭代

​ 不生成新的链表，把链表的指向的方向反过来

假设链表为 1 ->2 -> 3 ->∅ 1→2→3→∅，我们想要把它改成 ∅←1←2←3。

在遍历链表时，将当前节点的指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

1621751662409

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
  ListNode* reverseList(ListNode* head) {	
        ListNode* pre = nullptr;
    	ListNode* cur = head;
        while (cur)
    	{
    		ListNode* T = cur->next;
            cur->next =pre;
            pre =cur;
            cur = T;
    	}  //画图解决
        return pre;
  }
};

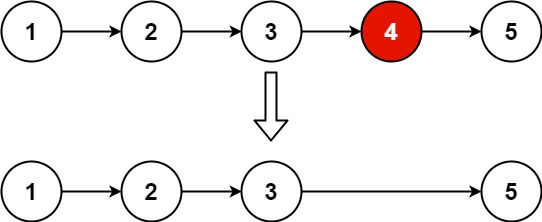
2.删除倒数第k个结点

​ 给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

img

1
2
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

解法一 ： 遍历整个链表后，算出结点数，反推正序第几个 O(N) N 为链表的长度 ，T（N)

解法二 ：双指针，一个前指针一个指针，前指针先走n步，然后 后指针和前指针一起走，前指针走到尾后，后指针指向待删除节点的前一部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* pre = new ListNode(1);  //设置一个虚拟的前置结点
		pre->next = head;
		ListNode* h1 = pre; //前指针
		ListNode* h2 = pre; //后指针
        ListNode* temp = nullptr; 
		for (int i = 0; i < n+1; ++i)
			h1 = h1->next;
		while (h1)
		{
			h1 = h1->next;
			h2 = h2->next;
		}	
	    temp = h2->next;
		h2->next = h2->next->next;
	    delete temp;
	    head = pre->next;
	    delete pre;
		return head;
	}
};

3.盛最多水的容器（双指针）

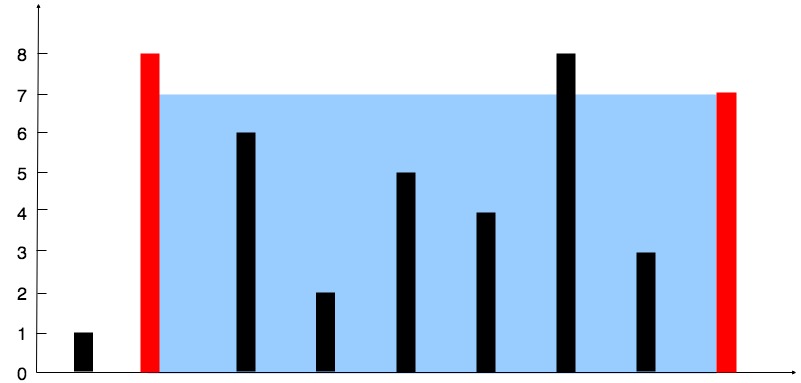
1
给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

img

1
2
3
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

解法一：暴力求解

​ 遍历每一个容器， 时间复杂度O（n^2)

解法二： 双指针

  • 一个指针在头，一个指针在后，分别向中间靠拢，如何移动呢（移动的条件）？

  • 那个指针指向的值比较小就先移动那个.

  • 容器的大小
    min（头，尾） * （头到尾直接的距离）
    为啥移动小的呢？
    容器的大小取决于最小的那个板，移动最大的那个板子，容器只会变得最小或者不变（板子可能变大，容器大小不变，板子变小若是比原来较小的那个板子还小，容器则会变得更小）移动较大的那个板子则是可能变大，会不会错过同个长度的其他搭配呢？其实我也没琢磨透…

  • 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int maxArea(vector<int>& height) {
		int l = 0, r = height.size() - 1;//减一是要换成逻辑地址下标
		int ans = 0; 
		while (l<r)
		{
			int area = min(height[l], height[r]) * (r - l);
			ans = max(ans, area);
			if (height[l] < height[r])
				l++;
			else
				r--;
		}
		return ans;
	}

4.冒泡排序

​ 今天去面试，笔试要写个冒泡排序，这题应该信手拈来的，可我还推了那么久！！不行啊！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> maopao(vector<int> x)
	{
		int i, y;
		for (i = 0; i < x.size() - 1; i++)
		{
			for ( y = 0; y < x.size()-1 - i; y++)
			{
				if (x[y] > x[y + 1])
				{
					swap(x[y], x[y + 1]);
				}
			}		
		}
		return x;
	}

时间复杂度为O( n^2） 两遍循环

5数组中重复的数字

1
2
3
4
找出数组中重复的数字。


在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
1
2
3
4
5
6
7
示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3


解法1 : 用set容器（该容器没有重复的数字），遍历vector ，遍历一个插入一个，插入失败则是重复的

1
2
3
4
5
6
7
 int findRepeatNumber(vector<int>& nums) {
 sort(nums.begin(), nums.end());		 	
 for (int x = 0; x < nums.size(); x++) 	
	if (nums[x] == nums[x + 1]) 	
		return nums[x + 1]; 
    return 0;    
};

解法2： 原地交换，有0- n-1个数字， 每个数都对应一个下标 i，当然 下标 i 不一定等于 nums[i],

若是等于的话，则有可能一个下标对应很多个数，

1622255058092

遍历每一个数，将其数值作为下标，即

1
nums[nums[i]] = nums[i];

这样一来就做到 数值就是其索引值

继续遍历 ，若是发现 交换时 索引值对应的数值已经存在了，则说明有重复的了

1
2
if (nums[nums[i]]== nums[i])
	return nums[i];

看代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int findRepeatNumber(vector<int>& nums) {
      int i = 0;
	while (i<nums.size())  //遍历
	{
		if (nums[i] == i)  //判断索引值和当前的值是否对应
		{
			i++;		//是，则继续遍历下一个
			continue;
		}	
		if (nums[nums[i]] == nums[i])  //核心： 判断是否有重复
               							//判断当前的值 和以当前值为索引的所对应的值是否相等
			return nums[i];
		swap(nums[i], nums[nums[i]]);	//不相等，则交换
		i++;
	}
	return -1;
   }

6.二叉树的三种遍历

递归 和迭代的方法

前序 （根左右）

递归：先往左边一直遍历，遍历一个抽一个，，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int forn_tree(TreeNode* root,vector<int>& res) {
		if (root = NULL)    //递归出口 该节点不存在
			return ;  //遍历每一个元素都是根节点
		res.push_back(root->val);  //遍历每一个元素都是根节点
		forn_tree(root->left, res);
		forn_tree(root->right, res);
		}
vector<int> preorderTraversal(TreeNode* root) {
	vector<int> res;
	forn_tree(root, res);  //递归函数
	return res;
}


利用栈来完成递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

vector<int> preorderTraversal(TreeNode* root) {
	vector<int> res;
		stack<TreeNode*> s;
		while (!s.empty() || root)
		{
			if (root)
			{
				res.push_back(root->val);
				s.push(root);
				root = root->left;
			}
			else
			{
				root = s.top();
				s.pop();
	    		root = root->right;
			}
		}
        return res;
	}

中序 （左根右）

同上，递归遍历，问题是何时打印出来该节点 总结：跟在哪里就先打印哪里，如中序 根在左右节点中间

所以， 先遍历左边，一直往左遍历，到最左边的时候打印节点，然后往右遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> inorderTraversal(TreeNode* root) {
		vector<int> res;
		inorderTraversal_tree(root, res);
		return res;
	}
	void inorderTraversal_tree(TreeNode* root, vector<int> &res) {
		if (root == nullptr)
			return ;
		inorderTraversal_tree(root->left, res);
		res.push_back(root->val);
		inorderTraversal_tree(root->right, res);

}

使用栈来递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<int> inorderTraversal(TreeNode* root) {
	vector<int> res;
	stack<TreeNode*> s;
	while (!s.empty() || root)
	{
		if (root)
		{
			s.push(root);
			root = root->left;
		}
		else
		{
			root = s.top();
			s.pop();
			res.push_back(root->val);
			root = root->right;
		}

	}
}

后续 （左右根）

原理同上

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> postorderTraversal(TreeNode* root) {
		vector<int> res;
		inorderTraversal_tree(root, res);
		return res;
	}
	void postorderTraversal_tree(TreeNode* root, vector<int> &res) {
		if (root == nullptr)
			return ;
		postorderTraversal_tree(root->left, res);
	
		postorderTraversal_tree(root->right, res);
        	res.push_back(root->val);
}

使用栈来递归：

1
2
3
4
5
6
vector<int> postorderTraversal(TreeNode* root) 
{
		vector<int> res;
		inorderTraversal_tree(root, res);
		return res;
}

7. 合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

思路：

​ 两个链表，建立一个新的头结点，每次比较两个链表当x较大小，那个小则头结点指向那个（尾插法），当前节点值小的链表则指向下一个节点，空间复杂度为O（1），没有用到额外的空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
 class Solution {

public:

  ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

    ListNode* preHead = new ListNode(-1);
    ListNode* prev = preHead;
	while (l1 != nullptr && l2 != nullptr) {
	if (l1->val < l2->val) {
		 prev->next = l1;
	     l1 = l1->next;
	    } else {
    prev->next = l2;
    l2 = l2->next;
   }
    prev = prev->next; //尾插法
  }
   // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
   prev->next = (l1 == nullptr ? l2 : l1);
    return preHead->next;
  }

8.合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

1
2
3
4
5
6
7
8
9
10
 输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

多个链表升序，也才用合并两个链表的思路来，用一个临时链表ans来保存两个链表合并后的结果，然后遍历每一个有序链表

没有用到额外的空间，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
  ListNode* twoLists1(ListNode* l1, ListNode* l2) {
		ListNode* preHead = new ListNode(-1);
		ListNode* prev = preHead;
		while (l1 != nullptr && l2 != nullptr) {
			if (l1->val < l2->val) {
				prev->next = l1;
				l1 = l1->next;
			}
			else {
				prev->next = l2;
				l2 = l2->next;
			}
			prev = prev->next; //尾插法
		}
		// 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
		prev->next = l1 == nullptr ? l2 : l1; //三则表达式   如果l1为空了，则l2还有
		return preHead->next;
	}
ListNode* mergeKLists(vector<ListNode*>& lists) {
	  ListNode *ans = nullptr;
		int len = lists.size();
		for (int i = 0; i < len; i++){
			ans = twoLists1(ans, lists[i]); //遍历每一个链表
		}
		return ans;

	}

9.有效的括号

1
2
3
4
5
6
7
给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

思路：

​ 利用堆栈的特性（FIFO） ，遍历字符串每一个元素时，逐个入栈，一定是左括号的先入栈

遍历到右括号则检查栈的顶部是否匹配，匹配则出栈，为了方便建立对应 哈希表 方便判断出 左右括号是否匹配，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
 
public:

  bool isValid(string s) {
    int x = 0, z = 0, d = 0;
    int n = s.size();   
    if (s.size() % 2 != 0) //括号肯定为偶数
      return false;
      //建立无序表 逐一做匹配
    unordered_map<char, char> pairs = {
    {')', '('},
    {']', '['},
     {'}', '{'}
    };
    stack<char> stk;
    for (auto ch : s) //遍历字符串元素
    {
      if (pairs.count(ch))  //判断改字符是否为右括号
      {
       if (stk.empty() || stk.top() != pairs[ch])  //若果栈空了或者栈顶的右括号和刚遍历的左括号不匹配则返回false
          return false;
        stk.pop(); //匹配成功则把出栈，把栈顶匹配完成的元素去掉
      }
     else {
        stk.push(ch);//没有遍历到右括号则出栈
      }
    }  
   return stk.empty();
  }
};

10. 斐波那契数列

1
2
3
4
5
写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

递归的接法：

​ 将大问题分解成若干个小问题

​ F(5)= F(4)+F(3);

​ F(4)=F(3)+F(2)…..

​ 以此类推

1
2
3
4
5
6
7
int fib(int n) {
	if (n <= 0)
		return 0;
	if (n == 1)
		return 1;
	return fib(n - 1) + fib(n - 2);
}

非递归的接法（从下往上，求出每个数 ,时间复杂度 O(n)）

1
2
3
4
5
6
7
8
9
10
11
12
13
int fib_1(int n) {
	int arr[2] = { 0,1 };
	int pre = 0;
	int now = 1;
	int next = 0;
	for (int i =2; i <= n; ++i)
	{
		next = pre + now;   //用next 保留两个数相加的和
		pre = now;			//pre 和 now 变量向前推进
		now = next;
	} 		
	return next;
}

也可以用以下的方法（和上面的思路一样，只是采用了数组的形式，很妙！）

1
2
3
4
5
6
7
8
9
int fib(int n) {
arr[2] = {0, 1};
   for(int i = 2; i <= n; ++i) {
     arr[i & 1] = (arr[0] + arr[1]) % (int)(1e9 + 7);
   }
   return arr[n & 1];  //n &1 的用意是： 定位到数组的小标 ， n&1 的值只能为 0 或 1
 }


11.青蛙跳台阶（和斐波那契数列一样）

1
2
3
4
一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

青蛙可以跳一步或者两步 顶一个函数 f（n） n表示台阶

​ 跳第一个台阶的时候，有一种选择 f(1)，跳第二台阶的时候 f(2) ，有两种选择，跳第三个的时候，第二台阶到第三个台阶只有一种选择–跳一个；第一个台阶到第三台阶跳两个，需要考虑的是当前阶梯数 n 和 n -2 和n与n-2之间的的数目 f（n） = f（n-1） +f ( n -2 )

f(3) = f(2)+f(1) 这样就是斐波那契数列啦，可以用递归，但重复计算很多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 int numWays(int n) {
  if(n ==0)
   	return 1;
  else if(n ==1)
    return 1;
  else if(n ==2)
    return 2;
  int pre = 1;
  int now = 2;
  int next = 0;
  for (int i =3; i <= n; ++i)
  {
      next = (pre + now)%(int(1e9+7));  //用next 保留两个数相加的和
 	  pre = now%(int(1e9+7));     //pre 和 now 变量向前推进
      now = next%(int(1e9+7));
  }    
  return next;
}

11.二分查找

二分查找是针对有序数列 的，对无序数列是无效的，在有序序列中使用二分查找能大大提高查找效率，通常能将时间按复杂度从 O(n)降至O(logn)

eg:

在一个有序数组中查找某个元素的位置

  • 递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int find_gui(vector<int>& nums, int target, int l, int r)
{
	int right = r;
	int left = l;
	int mid  = left + (right - left) / 2;		
	if (right < left)
		return -1;
	if (nums[mid] < target)
		se_gui(nums, target,mid + 1,r);
	else if (nums[mid] > target)
		se_gui(nums, target, l, mid- 1);
	else if(nums[mid] == target)
		return mid;		
}
  • 非递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- 
int search1(vector<int>& nums, int target) {
		int len = nums.size() - 1;
		int left = 0, right = len;
		int mid;
		while (left < right)
		{
			mid = left + (right - left) / 2;
			if (nums[mid] < target)
				left = mid + 1;
			else if (nums[mid] > target)
				right = mid - 1;
			else
				return mid;				
		}
		return -1;
	}

相关题目：

​ 在升序的序列中找到指定数字出现的次数

12.查找两个链表的相同节点（）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
	ListNode* At = headA;
	ListNode* Bt = headB;
	while (At!=Bt)
	{
		if (At != nullptr)
			At = At->next;
		else
        	At =headB;
        	
		if (Bt == nullptr)
			Bt = Bt->next;
		else
			Bt = headA;
	}
	return Bt;
}

13.排序大总结

快排（被问了好几次…）

复杂度是O（nlogn）

思路是：

​ 每一次的遍历把首元素放到他应该在的位置

如

1
5，1 ，4，3

​ 5 的位置应该是 在四位的，第一轮目标就时要包5 放在第四位，其他的不用管

其它的数字 经过一轮的排序后，会以选定数字的为轴，大的右边，小的在左边；

​ 以定位好的数字为轴，对左边的数字在重复一次以上的操作，对右边的也是，这就是用到递归了;

递归的层数越多是时间复杂度也越大， 平均的时间复杂度是 nO(logn)

n 代表层数， logn带边每层遍历的次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
vector<int> sortArray_1(vector<int>& nums) {
	int high = nums.size() - 1;
	QSort(nums, 0, high);
	return nums;
}
void QSort(vector<int> &nums,int low,int high)
{
	int mid;
	if (low < high)  
	{
		mid = Partition(nums, low, high);
		QSort(nums, low, mid - 1); //递归左边的
		QSort(nums, mid + 1,high); //递归右边的
	}
}
int Partition(vector<int>& nums,int low,int high)
{
	int r = high;
	int l = low;
	int std = nums[l]; //选定需要定位的目标数
	while (l < r)  //首尾各自开始向中心靠齐
	{
	//要从后面开始，判断数字是否大于目标数，知道遇到大于的
		while (l < r && nums[r] >= std)  
		{
			r--;
		}
		//然后交换数字
		swap(nums[l], nums[r]);
		//然后在来左边 
		while (l < r && nums[l] <= std)
		{
			l++;
		}//同理
		swap(nums[l], nums[r]);
	}

	return l;
}

14. 2n+1个数字，找出一个不对的数字

15.1000瓶药水有一瓶毒药，怎么快速检测出来（可用小白鼠）

讲一千瓶药水用二进制排序，2的10次方 为1024 故需要10位

00000 00000 1

00000 00001 2

00000 00010 3

…..

1111101000 1000

有10 位，我们用10只老鼠（每个老鼠都有编号 0-9）来检测， 瓶子序号中，第n位为1（n的取值为（0~9）） ，就用给对应编号为 n 的老鼠喝 如：

00001 00001 第0 位和第5位为1 ，则用调 编号 为 0 和 5的老去和药水

最后看是那些老鼠死了，死老鼠的序号，对应二进制的第几位，如 编号 二 和 三老鼠死了， 则二进制 为 0110 ，该编号对应的药水的编号，就是有毒的了

16.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

思路：

  • 暴力解法
    判断每个柱子能否装水，得看柱子左右两边的柱子 ，水的高度取决于最短的
    并且中间的柱子也有高度，所以也要减去当前柱子（即中间的柱子）的高度
    每一个柱子 装水量为
    ​ s = min（left，right） - mid
    总结： 遍历每一个柱子，取柱子左边最高的柱子，柱子右边最高的柱子，然后以左右两边最低的为标准来计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 class Solution {
public:
  int trap(vector<int>& height) {
  int n = height.size();
  int ans = 0;
  //遍历每一个柱子
  for (int i = 1; i < n - 1; i++) {
   int l_max = 0, r_max = 0;
    // 找右边最高的柱子
   for (int j = i; j < n; j++)
    r_max = max(r_max, height[j]);
    // 找左边最高的柱子
    for (int j = i; j >= 0; j--)
    l_max = max(l_max, height[j]);
    // 如果自己就是最高的话，
    // l_max == r_max == height[i]
    ans += min(l_max, r_max) - height[i];
  }
  return ans;
  }
};