LeetCode-树

Last updated on 8 months ago

1. 恢复二叉搜索树

给你二叉搜索树的根节点 root ，该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

思路：二叉搜索树中序排序是升序的，中序遍历时记录前一个节点，比较当前节点和上个节点，正常的树是当前节点要大于上一节点

class Solution {
public:
  TreeNode *t = nullptr;
  TreeNode *a = nullptr;
  TreeNode *b = nullptr;
  void backTree(TreeNode *root) {
    if (root->left != nullptr)
      backTree(root->left);
    //当前的值要大于上一个  二叉搜索数中序遍历是递增的
    if (t != nullptr && t->val > root->val) {
      if (a == nullptr) { //保存上一个节点
        a = t;
      }
      b = root;  //和当前的节点
    }
    t = root;
    // cout << root->val;
    if (root->right != nullptr) {
      backTree(root->right);
    }
  }
  void recoverTree(TreeNode *root) {
     backTree(root); //按照正常的中序遍历来处理
     swap(a->val,b->val);   //两个节点交换
  }
};

2 .树的前中后序遍历

递归排序：相对于递归比较简单，总体公式就是

确定递归的参数，返回值
递归终止的条件
递归的逻辑（前中还是先后）


//以下是 中序遍历
void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中  
    traversal(cur->right, vec); // 右
}
//后序遍历
void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}

递归可以的，用迭代一般都可以都可以:
使用一个栈来辅助

前序遍历：遍历第一个数进栈，然后出栈，出栈前，先看下他有无左右子树，有的话先进右节点，后进左节点，为什么呢？因为前序是先忘左边遍历的后面才往右边遍历

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root); //先进栈
        while (!st.empty()) {  //不为空
            TreeNode* node = st.top();                          // 中
            st.pop(); //出栈
            result.push_back(node->val); //保存结果
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return result;
    }
};

中序遍历：对于中序，有点特殊，遍历的结果是左右都没有节点的时候才是我们想要的节点，思路还是一样先一直往左走，走一个压栈一个，遇到没有左子节点的时候，看下有无右节点，没有则出栈（左中右），看其右边有无子节点

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};

后序遍历：前序遍历时是中左右，当然我们也可以中右左(改变遍历顺序)，将这个结果倒序排一遍就是后序遍历了…

3 .二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

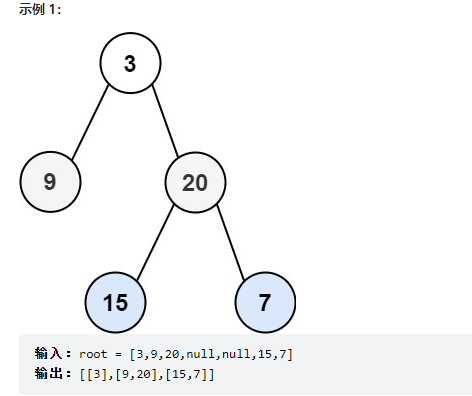
 ![image-20220321120854055](http://imt.rui.vin/202203211218012.png)

思路：会这题可以解决很多树的问题！

利用队列的性质，第一次进3，出队列，然后3的左右子树依次进队，此时队列里有9,10，让后重复出一个节点，然后该节点的左右节点分别进入，同理，10 节点也是一样

class Solution {
public:
   vector<vector<int>> levelOrder(TreeNode* root) {
	queue<TreeNode *> que;
	if(root != nullptr)
	    que.push(root);
	vector<vector<int>> res;
	vector<int> num;
	while (!que.empty()) {  //队列不为空则说明 还没遍历完
		int size = que.size(); //这里 记录当前要出队列的元素个数，出的时候也有进入，要先规定好出多少个
		for (int i = 0; i < size; i++) {
            TreeNode* node = que.front(); 
            que.pop();//出一个
            num.push_back(node->val);
            //出队列的左右子树入队列
            if (node->left) que.push(node->left); 
            if (node->right) que.push(node->right);
		}
		res.push_back(num);
		num.clear();
	}
	return res;
  }
};

层次遍历可以解决二叉树的层数也是可以解决，加一个变量记录进入for的次数，而且还可以记录出最小的高度，即节点的左右子节点都为空的时候

4. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

已知前序和中序推后序，很基础的题，但是用代码实现就有点困难了，应该是用递归，不知怎么递归，以及边界的处理

前序的每个数都将中序分为两部分，通过中序左右两部分个数又可以将前序分为两部分

简单的划分 ·

通过前序的值可以找到中序的下标索引然后在开始划分，左子树递归 和 右子树递归

为了方便通过前序值马上找到中序的下标，可以先用 map来索引

class Solution {
public:
    map<int,int> nodemap; //方便找 中序下标
    //每次递归 的参数包含  前序的起始坐标， 和 中序的起始坐标
    TreeNode* drawback(vector<int>& preorder, vector<int>& inorder,int Pleft,int Pright,int Ileft,int Iright){
        if(Pleft > Pright)
            return nullptr;
        int preroot = preorder[Pleft]; // 每次去前序的第一个值
        int inroot = nodemap[preroot]; //通过 map 找到 中序的索引
        TreeNode *root = new TreeNode(preroot);  // 当前 前序的值就头结点 

        int size_left_node = inroot - Ileft;   //要划分 前序 的左右部分， 通过中序可以知道前序的左部分多少个数，即可求出前序的分界值
        //左子树
        root->left = drawback(preorder,inorder,Pleft+1,Pleft+size_left_node,Ileft,inroot-1);
		//右子树
        root->right = drawback(preorder,inorder,Pleft+size_left_node+1,Pright,inroot+1,Iright);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(!preorder.size() || !inorder.size()){
            return nullptr;
        }
        for(int i = 0; i < inorder.size();i++ ){
            nodemap[inorder[i]] = i;
        }

      return  drawback(preorder,inorder,0,inorder.size()-1,0,inorder.size()-1);
    }
};

5. 二叉树中的最大路径和

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

树的问题往往都是用递归来解决，这次递归麻烦

如上图，路径是 15 - 20 - 7 的值最大，不需要打印出路劲节点，只需求最大值，把问题细分下去对于每一个节点都可以看做是一个根节点

对于一个小树，有几种可能呢，一种是路劲都走完有最大值，还有一种是三个节点中取一个节点作为最大值

同理，对于根节点为10 的树（他的全部节点抽象成左右两个节点），同理也是有两种取法

现在问题就可以推倒求一个子树的最大路径值，路劲都是左中右，中序遍历

递归的参数是每个叶子节点

递归的出口是叶子结点为空

递归的逻辑是左到右

做一个全局变量，用于取最大值

class Solution {
public:
    int maxsum = INT_MIN;
    int getMax(TreeNode *root){
		//递归出口
        if(root == nullptr){
            return 0;
        }
        //递归左边子树 ，返回最后一左节点值
        int lval = max(getMax(root->left),0);
        //同上
        int rval = max(getMax(root->right),0);
	   //第一种路径选择  从左到右，逐个走，用全局变量记录 	
        maxsum = max(root->val + lval + rval,maxsum);
	   //第二种 根节点加上 左右两个节点最大哪个
        return root->val + max(lval,rval);
    }
    int maxPathSum(TreeNode* root) {
        getMax(root);
        return maxsum;
    }
};

#树

LeetCode-堆栈问题 Previous

LeetCode-树 Next